Уравнение регрессии
Назначение сервиса. С помощью сервиса в онлайн режиме можно найти:- параметры уравнения линейной регрессии
y=a+bx, линейный коэффициент корреляции с проверкой его значимости; - тесноту связи с помощью показателей корреляции и детерминации, МНК-оценку, статическую надежность регрессионного моделирования с помощью F-критерия Фишера и с помощью t-критерия Стьюдента, доверительный интервал прогноза для уровня значимости α
см. также сервис
Корреляционная таблица.
При количестве данных больше 100, создается только шаблон решения в MS Excel. Если требуется построить сразу несколько уравнений регрессии и найти лучшее из них, то можно воспользоваться сервисом
Регрессионный анализ в Excel.
Для получения обратного уравнения регрессии
x=by+a, достаточно вставить данные в обратном порядке (первый столбец Y, второй столбец X).

Типовые задания
Исследуется зависимость производительности труда y от уровня механизации работ x (%) по данным 14 промышленных предприятий. Статистические данные приведены в таблице.
Требуется:
1) Найти оценки параметров линейной регрессии у на х. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
2) На уровне значимости α=0.05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
3) С надежностью γ=0.95 найти доверительные интервалы для параметров линейной регрессии.
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии:  . Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel
. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel
Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.
Пример. Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели - определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x, т. е. модель вида:
Графически покажем регрессионную зависимость между выработкой продукции на одного работника и удельного веса рабочих высокой квалификации.
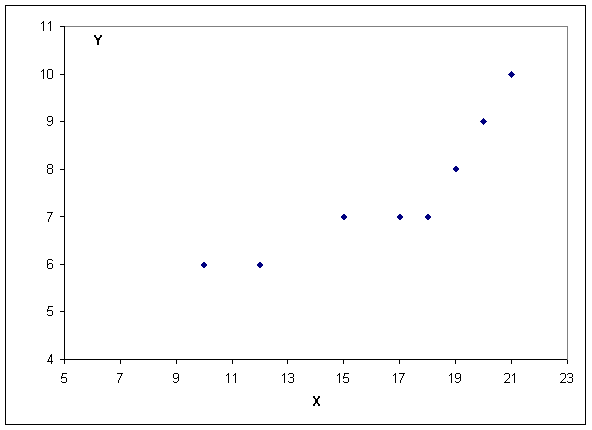
3-й этап (параметризация) – собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными. Выбор вида функциональной зависимости в уравнении регрессии называется параметризацией модели. Выбираем уравнение парной регрессии, т.е. на конечный результат y будет влиять только один фактор.
4-й этап (информационный) – сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей. Выборка состоит из 10 предприятий отрасли.
5-й этап (идентификация модели) – оценивание неизвестных параметров модели по имеющимся статистическим данным.
Чтобы определить параметры модели, используем МНК - метод наименьших квадратов. Система нормальных уравнений будет выглядеть следующим образом:
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для расчета параметров регрессии построим расчетную таблицу (табл. 1).
| x | y | x2 | y2 | x • y |
| 10 | 6 | 100 | 36 | 60 |
| 12 | 6 | 144 | 36 | 72 |
| 15 | 7 | 225 | 49 | 105 |
| 17 | 7 | 289 | 49 | 119 |
| 18 | 7 | 324 | 49 | 126 |
| 19 | 8 | 361 | 64 | 152 |
| 19 | 8 | 361 | 64 | 152 |
| 20 | 9 | 400 | 81 | 180 |
| 20 | 9 | 400 | 81 | 180 |
| 21 | 10 | 441 | 100 | 210 |
| 171 | 77 | 3045 | 609 | 1356 |
Данные берем из таблицы 1 (последняя строка), в итоге имеем:
10a + 171 b = 77
171 a + 3045 b = 1356
Эту СЛАУ решаем методом Крамера или методом обратной матрицы.
Получаем эмпирические коэффициенты регрессии:
b = 0.3251, a = 2.1414
Эмпирическое уравнение регрессии имеет вид:
y = 0.3251 x + 2.1414
6-й этап (верификация модели) – сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.
Анализ проводим с помощью проверки адекватности модели и с помощью статистической значимости параметров парной регрессии.