Калькулятор по химии
- вещественные числа оформляются через разделитель точку (например, 0.25).
- перед каждым показателем указывается его наименование, например, давления p2=0.5 МПа, температура t=50 C.
Примеры.
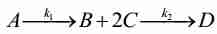 | A -->|k1| B+2*C B+2*C -->|k2| D |
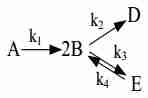 | A -->|k1| 2B 2B -->|k2| D 2B -->|k3| E E -->|k4| 2B |
 | A -->|k1| 2B A -->|k2| C+E C+E -->|k3| D |
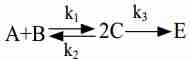 записываем формализованное условие:
записываем формализованное условие:
Написать кинетическое уравнение для химической реакции:
A+B -->|k1| 2C
2C -->|k2| A+B
2C -->|k3| E
Пример
Исходные концентрации оксида азота (II) и хлора в системе 2NO + Cl2 ↔ 2NOCl составляют соответственно 0,5 моль/дм3 и 0,2 моль/дм3. Вычислите константу равновесия, если к моменту наступления равновесия прореагировало 25% оксида азота (II).Формализованное задание:
Исходные концентрации оксида азота (II) и хлора в системе 2*NO + Cl2 = 2*NOCl составляют соответственно 0.5 моль/дм^3 и 0.2 моль/дм^3. Вычислите константу равновесия, если к моменту наступления равновесия прореагировало 25% оксида азота (II).
Важно! Решение, полученное нейросетями AI могут содержать ошибки.
Примеры решения задач по химии
Задание. Сколько граммов хлорида натрия нужно растворить в 500 г. воды, чтобы получить 0.5%-й молярный раствор?
Решение.
Определения:
- Массовый процент (w/w%) — это отношение массы растворённого вещества к общей массе раствора, умноженное на 100.
- Молярный раствор (M) — это количество молей растворённого вещества в 1 литре раствора.
1. Молярная масса NaCl:
Na = 23 г/моль
Cl = 35.5 г/моль
M(NaCl) = 23 + 35.5 = 58.5 г/моль
2. Молярность (M) — это количество молей вещества в 1 литре раствора: 0.5 M = 0.5 моль NaCl / 1 л раствора
3. Объём раствора:
Вода = 500 г
Плотность воды ≈ 1 г/мл → 500 г воды = 500 мл = 0.5 л
Но раствор — это вода + NaCl, поэтому объём раствора немного больше 0.5 л. Однако, если масса NaCl мала по сравнению с массой воды, можно приближённо считать, что объём раствора ≈ 0.5 л.
4. Моли NaCl в 0.5 л 0.5 M раствора: 0.5 моль/л × 0.5 л = 0.25 моль NaCl
5. Масса NaCl: 0.25 моль × 58.5 г/моль = 14.625 г
Ответ:
Чтобы приготовить 0.5-молярный раствор NaCl в 500 г воды, нужно растворить примерно 14.6 г NaCl.
Покажем расчет при 0.5%-м по массе растворе:
- 0.5% — это 0.5 г NaCl на 100 г раствора
- В 500 г раствора будет: $ \frac{0.5}{100} \times 500 = 2.5 $ г NaCl
Задание. Какая масса ртути содержалась в 250 мл раствора, если после прибавления к 50 мл его 25 мл 0.01000 М раствора ЭДТА избыток последнего оттитровали 10.5 мл 0.01000 М MgSO4?
Решение.
Задание. Написать кинетическое уравнение для реакции:
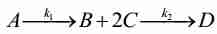
Решение.
- A — исходное вещество
- B и C — промежуточные вещества
- D — продукт
- $[A] = c_A$
- $[B] = c_B$
- $[C] = c_C$
- $[D] = c_D$
$k_1$ — скорость прямой реакции $A \rightarrow B + 2C$
$k_2$ — скорость обратной реакции $B + 2C \rightarrow D$
Кинетические уравнения
Скорости изменения концентраций веществ: $$ \frac{d[A]}{dt} = -k_1 [A] $$ $$ \frac{d[B]}{dt} = k_1 [A] - k_2 [B][C]^2 $$ $$ \frac{d[C]}{dt} = 2k_1 [A] - 2k_2 [B][C]^2 $$ $$ \frac{d[D]}{dt} = k_2 [B][C]^2 $$ Объяснение:
- Реакция $A \rightarrow B + 2C$ первого порядка по A → скорость равна $k_1 [A]$.
- Реакция $B + 2C \rightarrow D$ второго порядка по суммарной концентрации (первый порядок по B, второй порядок по C) → скорость равна $k_2 [B][C]^2$.
- Изменение концентраций учитывает стехиометрию: на каждую молекулу B приходится две молекулы C.
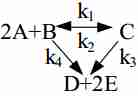
Задание. В химическом реакторе высотой 25 м диаметром трубки 0.05 м протекает химическая реакция:
Записать математическую модель процесса.
Решение.
- Геометрию реактора (высота 25 м, диаметр трубки 0.05 м — это указывает на трубчатый реактор);
- Кинетику реакций;
- Распределение концентраций по длине реактора (т.к. это трубчатый реактор, модель строится в режиме идеального вытеснения — ИВ).
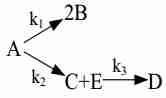
- $ 2A + B \xrightarrow{k_1} C $
- $ C \xrightarrow{k_2} 2A + B $
- $ C \xrightarrow{k_3} D + 2E $
- $ 2A + B \xrightarrow{k_4} D + 2E $
Для трубчатого реактора при идеальном вытеснении и стационарном режиме, математическая модель описывается системой обыкновенных дифференциальных уравнений (ОДУ) по длине реактора $ z \in [0, L] $, где $ L = 25 $ м.
Баланс вещества для компонента $ i $: $$ \frac{dC_i}{dz} = \frac{1}{u} \cdot \sum_j \nu_{i,j} r_j $$ где:
- $ u $ — линейная скорость потока (м/с),
- $ \nu_{i,j} $ — стехиометрический коэффициент $ i $-го вещества в $ j $-й реакции,
- $ r_j $ — скорость $ j $-й реакции.
Дифференциальные уравнения модели.
Объединяем все реакции:
Для A: $$ \frac{dC_A}{dz} = \frac{1}{u} \left[ -2r_1 + 2r_2 - 2r_4 \right] = \frac{1}{u} \left[ -2k_1 C_A^2 C_B + 2k_2 C_C - 2k_4 C_A^2 C_B \right] $$ $$ \Rightarrow \boxed{\frac{dC_A}{dz} = \frac{-2(k_1 + k_4) C_A^2 C_B + 2k_2 C_C}{u}} $$ Для B: $$ \frac{dC_B}{dz} = \frac{1}{u} \left[ -r_1 + r_2 - r_4 \right] = \frac{1}{u} \left[ -k_1 C_A^2 C_B + k_2 C_C - k_4 C_A^2 C_B \right] $$ $$ \Rightarrow \boxed{\frac{dC_B}{dz} = \frac{-(k_1 + k_4) C_A^2 C_B + k_2 C_C}{u}} $$ Для C: $$ \frac{dC_C}{dz} = \frac{1}{u} \left[ r_1 - r_2 - r_3 \right] = \frac{1}{u} \left[ k_1 C_A^2 C_B - k_2 C_C - k_3 C_C \right] $$ $$ \Rightarrow \boxed{\frac{dC_C}{dz} = \frac{k_1 C_A^2 C_B - (k_2 + k_3) C_C}{u}} $$ Для D: $$ \frac{dC_D}{dz} = \frac{1}{u} \left[ r_3 + r_4 \right] = \frac{1}{u} \left[ k_3 C_C + k_4 C_A^2 C_B \right] $$ $$ \Rightarrow \boxed{\frac{dC_D}{dz} = \frac{k_3 C_C + k_4 C_A^2 C_B}{u}} $$ Для E: $$ \frac{dC_E}{dz} = \frac{1}{u} \left[ 2r_3 + 2r_4 \right] = \frac{2}{u} \left[ k_3 C_C + k_4 C_A^2 C_B \right] $$ $$ \Rightarrow \boxed{\frac{dC_E}{dz} = \frac{2(k_3 C_C + k_4 C_A^2 C_B)}{u}} $$ Начальные условия: задаются на входе реактора ($ z = 0 $): $$ C_A(0) = C_{A0}, \quad C_B(0) = C_{B0}, \quad C_C(0) = 0, \quad C_D(0) = 0, \quad C_E(0) = 0 $$ (Если начальная смесь содержит только A и B.)
📌 Примечания
- Если известны плотность и массовый расход, можно рассчитать $ u $ через объемный расход: $$ u = \frac{Q}{\pi (d/2)^2} $$
- Все концентрации имеют размерность [моль/м³], скорости реакций — [моль/(м³·с)], $ u $ — [м/с].
Цели и задачи изучения дисциплины химии
Цель дисциплины – формирование системы фундаментальных знаний по химии.Задачи изучения дисциплины
- изучить основные химические явления, овладеть фундаментальными понятиями, законами и теориями классической и современной химии;
- сформировать основы научного мировоззрения и современного химического мышления; ознакомиться с научной аппаратурой и методами химического исследования, приобрести навыки проведения химического эксперимента;
- научиться выделять химическое содержание в прикладных задачах будущей деятельности;
- овладеть методами решения инженерных задач.
Структура дисциплины химии
- Основы строения вещества.
- Взаимодействия веществ.
- Растворы.
- Электрохимические процессы.
- Реакционная способность веществ. Химические свойства металлов.
- Элементы органической химии.