Дискретная математика / Множества
Множества
С помощью калькулятора по заданному отношению определяются его свойства. См. примеры решений №1 и №2.
Область определения
С помощью калькулятора по заданному бинарному отношению определяются его свойства. См. пример решения.
Отношение задано в виде:
Примеры отношений множеств:
Примеры отображений: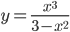
(х –у) кратно 3,
y2+x2≤16,
прямые l и m пересекаются,
х – сын у,
векторы a и b сонаправлены.
Примеры отображений:
(y+3)2+(x-2)2=16,
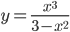
Примеры области определения: N, R, Z, [0,3],
векторы на плоскости,
жители города,
студенты,
читатели библиотеки.
Примеры области значения: R, (0; ∞), [-2,4], [0; π]. Указывается для отображений, заданных в виде уравнений.
Ввод матрицы. В каждой строке через пробел указывается элемент матрицы. Например:
1 0 1 1
1 1 1 0
1 0 1 1
1 1 1 0
Ввод графа. Формат ввода для неориентированного ребра vi-vj.
1-2
1-3
2-4
Формат ввода ориентированного ребра vi->vj. Например:
1->2
2->3
1->3
Важно! Решение, полученное нейросетями AI могут содержать ошибки.
Основные определения
Z - множество целых чисел (например, -1, 9), N - множество натуральных чисел (например, 1, 23), U (I) - универсальное множество.Соответствие f, сопоставляющее каждому элементу х из множества Х один и только один элемент из множества Y, называется однозначным отображением множества Х во множество Y. Множество А называется областью определения отображения f, а множество f(А) называется множеством значений этого отображения.
Бинарные отношения - отношения между элементами двух множеств.
Свойства отношений множеств
- Рефлексивность.
- Нерефлексивность.
- Симметричность.
- Антисимметричность.
- Транзитивность.
- Связность.
- Рефлексивное, антисимметричное и транзитивное отношение называется отношением частичного порядка.
- Связное отношение частичного порядка называется отношением линейного порядка.
- Нерефлексивное, антисимметричное и транзитивное отношение называется отношением строгого порядка.
- Связное отношение строгого порядка называется отношением строгого линейного порядка.
- Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
Свойства отображений множеств
- Сюръективное.
- Инъективное.
Пример №1. Рассмотрим бинарное отношение $ R $ на множестве натуральных чисел $ \mathbb{N} $, заданное условием:
$ xRy \iff (x - y) $ кратно 3.
То есть:
$$
xRy \iff x - y \equiv 0 \pmod{3}
$$
Обозначим это отношение как $ R $. Исследуем его свойства.
1. Рефлексивность Отношение рефлексивно, если для любого $ x \in \mathbb{N} $ выполняется $ xRx $. Проверка: $$ x - x = 0,\quad 0 \text{ кратно } 3 \Rightarrow xRx. $$ ✅ Выполняется. Рефлексивно.
2. Симметричность Отношение симметрично, если из $ xRy $ следует $ yRx $. Если $ x - y \equiv 0 \pmod{3} $, то $ y - x = -(x - y) \equiv 0 \pmod{3} $.
✅ Выполняется. Симметрично.
3. Транзитивность Отношение транзитивно, если из $ xRy $ и $ yRz $ следует $ xRz $. Допустим $ x - y \equiv 0 \pmod{3} $ и $ y - z \equiv 0 \pmod{3} $. Сложим эти два выражения: $$ (x - y) + (y - z) = x - z \equiv 0 \pmod{3}. $$
✅ Выполняется. Транзитивно.
4. Антирефлексивность Не выполняется, так как $ xRx $ истинно (например, $ 3 - 3 = 0 $).
❌ Не выполняется.
5. Антисимметричность Отношение антисимметрично, если из $ xRy $ и $ yRx $ следует $ x = y $. Но здесь: $ xRy \land yRx \Rightarrow x - y \equiv 0 \pmod{3} $, но это не означает, что $ x = y $, например: $ x = 6, y = 3 \Rightarrow 6 - 3 = 3 \equiv 0 \pmod{3} $, но $ x \ne y $.
❌ Не выполняется.
6. Итог Отношение $ R $ обладает следующими свойствами:
✅ Рефлексивность
✅ Симметричность
✅ Транзитивность Это значит, что отношение является отношением эквивалентности на множестве $ \mathbb{N} $. Ответ: Отношение "разность кратна 3" на множестве натуральных чисел является отношением эквивалентности.
Пример №2. Определить свойства отображения $y=3*sin(pi*x/2)$. Область определения: [0,1]. Область значений: [0,3]. Решение. Рассмотрим отображение: $$ y = 3 \sin\left(\frac{\pi x}{2}\right), \quad \text{где } x \in [0, 1] $$ 1. Область определения (domain): Указано: $ x \in [0, 1] $. Функция синуса определена на всей области вещественных чисел, так что в данном случае область определения — это заданный интервал.
2. Область значений (range): Рассмотрим поведение функции на заданном интервале:
При $ x = 0 $: $$ y = 3 \sin\left( \frac{\pi \cdot 0}{2} \right) = 3 \sin(0) = 0 $$
При $ x = 1 $: $$ y = 3 \sin\left( \frac{\pi \cdot 1}{2} \right) = 3 \sin\left( \frac{\pi}{2} \right) = 3 \cdot 1 = 3 $$ Синус строго возрастает на интервале $[0, \frac{\pi}{2}]$, значит, функция $ y = 3 \sin\left( \frac{\pi x}{2} \right) $ строго возрастает на $[0, 1]$. Таким образом, она принимает все значения от $ 0 $ до $ 3 $.
3. Инъективность (взаимная однозначность): Функция строго возрастает на всем интервале $[0, 1]$, т.е. если $ x_1 < x_2 $, то $ y(x_1) < y(x_2) $. Значит, разным аргументам соответствуют разные значения функции.
Вывод: отображение инъективно
4. Сюръективность (отображение "на"): Мы знаем, что функция принимает все значения из $[0, 3]$, и область значений совпадает с заданным множеством $[0, 3]$. Значит, для каждого $ y \in [0, 3] $ существует $ x \in [0, 1] $, такой что $ y = f(x) $.
Вывод: отображение сюръективно
5. Биективность: Если отображение одновременно инъективно и сюръективно, то оно является биекцией. Вывод: отображение биективно.
6. Непрерывность: Функция $ y = 3 \sin\left( \frac{\pi x}{2} \right) $ — композиция непрерывных функций (синуса и линейной функции), поэтому она непрерывна на всей области определения.
Вывод: функция непрерывна на $[0, 1]$
7. Монотонность: Как уже было установлено, функция строго возрастает на $[0, 1]$, поскольку синус возрастает на первом квадранте.
Вывод: функция строго возрастает на $[0, 1]$
Итог:
Обратная функция будет:
$$
x = \frac{2}{\pi} \arcsin\left( \frac{y}{3} \right), \quad y \in [0, 3]
$$
1. Рефлексивность Отношение рефлексивно, если для любого $ x \in \mathbb{N} $ выполняется $ xRx $. Проверка: $$ x - x = 0,\quad 0 \text{ кратно } 3 \Rightarrow xRx. $$ ✅ Выполняется. Рефлексивно.
2. Симметричность Отношение симметрично, если из $ xRy $ следует $ yRx $. Если $ x - y \equiv 0 \pmod{3} $, то $ y - x = -(x - y) \equiv 0 \pmod{3} $.
✅ Выполняется. Симметрично.
3. Транзитивность Отношение транзитивно, если из $ xRy $ и $ yRz $ следует $ xRz $. Допустим $ x - y \equiv 0 \pmod{3} $ и $ y - z \equiv 0 \pmod{3} $. Сложим эти два выражения: $$ (x - y) + (y - z) = x - z \equiv 0 \pmod{3}. $$
✅ Выполняется. Транзитивно.
4. Антирефлексивность Не выполняется, так как $ xRx $ истинно (например, $ 3 - 3 = 0 $).
❌ Не выполняется.
5. Антисимметричность Отношение антисимметрично, если из $ xRy $ и $ yRx $ следует $ x = y $. Но здесь: $ xRy \land yRx \Rightarrow x - y \equiv 0 \pmod{3} $, но это не означает, что $ x = y $, например: $ x = 6, y = 3 \Rightarrow 6 - 3 = 3 \equiv 0 \pmod{3} $, но $ x \ne y $.
❌ Не выполняется.
6. Итог Отношение $ R $ обладает следующими свойствами:
✅ Рефлексивность
✅ Симметричность
✅ Транзитивность Это значит, что отношение является отношением эквивалентности на множестве $ \mathbb{N} $. Ответ: Отношение "разность кратна 3" на множестве натуральных чисел является отношением эквивалентности.
Пример №2. Определить свойства отображения $y=3*sin(pi*x/2)$. Область определения: [0,1]. Область значений: [0,3]. Решение. Рассмотрим отображение: $$ y = 3 \sin\left(\frac{\pi x}{2}\right), \quad \text{где } x \in [0, 1] $$ 1. Область определения (domain): Указано: $ x \in [0, 1] $. Функция синуса определена на всей области вещественных чисел, так что в данном случае область определения — это заданный интервал.
2. Область значений (range): Рассмотрим поведение функции на заданном интервале:
При $ x = 0 $: $$ y = 3 \sin\left( \frac{\pi \cdot 0}{2} \right) = 3 \sin(0) = 0 $$
При $ x = 1 $: $$ y = 3 \sin\left( \frac{\pi \cdot 1}{2} \right) = 3 \sin\left( \frac{\pi}{2} \right) = 3 \cdot 1 = 3 $$ Синус строго возрастает на интервале $[0, \frac{\pi}{2}]$, значит, функция $ y = 3 \sin\left( \frac{\pi x}{2} \right) $ строго возрастает на $[0, 1]$. Таким образом, она принимает все значения от $ 0 $ до $ 3 $.
3. Инъективность (взаимная однозначность): Функция строго возрастает на всем интервале $[0, 1]$, т.е. если $ x_1 < x_2 $, то $ y(x_1) < y(x_2) $. Значит, разным аргументам соответствуют разные значения функции.
Вывод: отображение инъективно
4. Сюръективность (отображение "на"): Мы знаем, что функция принимает все значения из $[0, 3]$, и область значений совпадает с заданным множеством $[0, 3]$. Значит, для каждого $ y \in [0, 3] $ существует $ x \in [0, 1] $, такой что $ y = f(x) $.
Вывод: отображение сюръективно
5. Биективность: Если отображение одновременно инъективно и сюръективно, то оно является биекцией. Вывод: отображение биективно.
6. Непрерывность: Функция $ y = 3 \sin\left( \frac{\pi x}{2} \right) $ — композиция непрерывных функций (синуса и линейной функции), поэтому она непрерывна на всей области определения.
Вывод: функция непрерывна на $[0, 1]$
7. Монотонность: Как уже было установлено, функция строго возрастает на $[0, 1]$, поскольку синус возрастает на первом квадранте.
Вывод: функция строго возрастает на $[0, 1]$
Итог:
| Свойство | Результат |
| Область определения | $[0, 1]$ |
| Область значений | $[0, 3]$ |
| Инъективность | ✅ Да |
| Сюръективность | ✅ Да |
| Биективность | ✅ Да |
| Непрерывность | ✅ Да |
| Монотонность | ✅ Строго возрастает |
Пример №3. Определить свойства (рефлексивность,симметричность,транзитивность) бинарного отношения, заданного в виде матрицы:
$$
M_R =
\begin{bmatrix}
1 & 1 & 0 & 1 \\
1 & 1 & 1 & 0 \\
0 & 1 & 1 & 0 \\
1 & 0 & 0 & 0
\end{bmatrix}
$$
Элемент матрицы $ M_{ij} = 1 $ означает, что $ (a_i, a_j) \in R $, то есть элемент $ a_i $ связан с элементом $ a_j $.
1. Рефлексивность.
Отношение рефлексивно, если для всех $ i $ выполняется $ (a_i, a_i) \in R $, т.е. все диагональные элементы матрицы равны 1.
Диагональ матрицы: $ M_{11} = 1,\ M_{22} = 1,\ M_{33} = 1,\ M_{44} = 0 $
Вывод: отношение не рефлексивно, так как $ M_{44} = 0 $.
2. Симметричность.
Отношение симметрично, если из $ (a_i, a_j) \in R $ следует $ (a_j, a_i) \in R $, т.е. матрица должна быть симметричной относительно главной диагонали: $ M_{ij} = M_{ji} $.
Проверим несколько пар:
$ M_{12} = 1,\ M_{21} = 1 $ → ОК
$ M_{13} = 0,\ M_{31} = 0 $ → ОК
$ M_{14} = 1,\ M_{41} = 1 $ → ОК
$ M_{23} = 1,\ M_{32} = 1 $ → ОК
$ M_{24} = 0,\ M_{42} = 0 $ → ОК
$ M_{34} = 0,\ M_{43} = 0 $ → ОК
Все пары симметричны - отношение симметрично.
3. Транзитивность.
Отношение транзитивно, если из $ (a_i, a_j) \in R $ и $ (a_j, a_k) \in R $ следует $ (a_i, a_k) \in R $.
Это можно проверить через умножение матрицы отношения на себя: если $ M_R^2[i,k] > 0 $, то существует путь длины 2 из $ i $ в $ k $. Если при этом $ M_R[i,k] = 0 $, то отношение не транзитивно.
Вычислим $ M_R^2 = M_R \cdot M_R $: $$ M_R^2 = \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} (1+1+0+1)=3 & (1+1+0+0)=2 & (0+1+0+0)=1 & (1+0+0+0)=1 \\ (1+1+0+0)=2 & (1+1+1+0)=3 & (0+1+1+0)=2 & (1+0+0+0)=1 \\ (0+1+0+0)=1 & (0+1+1+0)=2 & (0+1+1+0)=2 & (0+0+0+0)=0 \\ (1+0+0+0)=1 & (1+0+0+0)=1 & (0+0+0+0)=0 & (1+0+0+0)=1 \end{bmatrix} $$ $$ M_R^2 = \begin{bmatrix} 3 & 2 & 1 & 1 \\ 2 & 3 & 2 & 1 \\ 1 & 2 & 2 & 0 \\ 1 & 1 & 0 & 1 \end{bmatrix} $$ Теперь сравниваем $ M_R^2[i,k] > 0 $ с $ M_R[i,k] = 0 $. Если есть такие случаии — отношение не транзитивно.
Например:
$ M_R^2[3,4] = 0 $, $ M_R[3,4] = 0 $ → OK
$ M_R^2[4,3] = 0 $, $ M_R[4,3] = 0 $ → OK
$ M_R^2[3,1] = 1 $, $ M_R[3,1] = 0 $ → Нарушение!
Есть путь из 3 в 1 через промежуточный элемент, но сама связь отсутствует ⇒ отношение не транзитивно.
Итог:
1. Рефлексивность.
Отношение рефлексивно, если для всех $ i $ выполняется $ (a_i, a_i) \in R $, т.е. все диагональные элементы матрицы равны 1.
Диагональ матрицы: $ M_{11} = 1,\ M_{22} = 1,\ M_{33} = 1,\ M_{44} = 0 $
Вывод: отношение не рефлексивно, так как $ M_{44} = 0 $.
2. Симметричность.
Отношение симметрично, если из $ (a_i, a_j) \in R $ следует $ (a_j, a_i) \in R $, т.е. матрица должна быть симметричной относительно главной диагонали: $ M_{ij} = M_{ji} $.
Проверим несколько пар:
$ M_{12} = 1,\ M_{21} = 1 $ → ОК
$ M_{13} = 0,\ M_{31} = 0 $ → ОК
$ M_{14} = 1,\ M_{41} = 1 $ → ОК
$ M_{23} = 1,\ M_{32} = 1 $ → ОК
$ M_{24} = 0,\ M_{42} = 0 $ → ОК
$ M_{34} = 0,\ M_{43} = 0 $ → ОК
Все пары симметричны - отношение симметрично.
3. Транзитивность.
Отношение транзитивно, если из $ (a_i, a_j) \in R $ и $ (a_j, a_k) \in R $ следует $ (a_i, a_k) \in R $.
Это можно проверить через умножение матрицы отношения на себя: если $ M_R^2[i,k] > 0 $, то существует путь длины 2 из $ i $ в $ k $. Если при этом $ M_R[i,k] = 0 $, то отношение не транзитивно.
Вычислим $ M_R^2 = M_R \cdot M_R $: $$ M_R^2 = \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} (1+1+0+1)=3 & (1+1+0+0)=2 & (0+1+0+0)=1 & (1+0+0+0)=1 \\ (1+1+0+0)=2 & (1+1+1+0)=3 & (0+1+1+0)=2 & (1+0+0+0)=1 \\ (0+1+0+0)=1 & (0+1+1+0)=2 & (0+1+1+0)=2 & (0+0+0+0)=0 \\ (1+0+0+0)=1 & (1+0+0+0)=1 & (0+0+0+0)=0 & (1+0+0+0)=1 \end{bmatrix} $$ $$ M_R^2 = \begin{bmatrix} 3 & 2 & 1 & 1 \\ 2 & 3 & 2 & 1 \\ 1 & 2 & 2 & 0 \\ 1 & 1 & 0 & 1 \end{bmatrix} $$ Теперь сравниваем $ M_R^2[i,k] > 0 $ с $ M_R[i,k] = 0 $. Если есть такие случаии — отношение не транзитивно.
Например:
$ M_R^2[3,4] = 0 $, $ M_R[3,4] = 0 $ → OK
$ M_R^2[4,3] = 0 $, $ M_R[4,3] = 0 $ → OK
$ M_R^2[3,1] = 1 $, $ M_R[3,1] = 0 $ → Нарушение!
Есть путь из 3 в 1 через промежуточный элемент, но сама связь отсутствует ⇒ отношение не транзитивно.
Итог:
- Рефлексивность**: ❌ Не выполнено
- Симметричность**: ✅ Выполнено
- Транзитивность**: ❌ Не выполнено