Задача потребительского выбора
Уровень удовлетворения материальных потребностей общества (уровень потребления) можно выразить целевой функцией потребления U = U(X) (функция полезности), где вектор переменных X>0 включает разнообразные виды товаров и услуг.Назначение сервиса. Сервис предназначен для нахождения функции спроса с помощью функции Лагранжа: L(X,λ) = U(X) + λ(D - P*X)
где множитель Лагранжа λ является оптимальной оценкой дохода.
Полученное решение сохраняется в файле Word (см. примеры решений).
Находятся предельные полезные эффекты (предельные полезности) соответствующих потребительских благ: ![]()
- Все переменные выражаются через x1,x2
- Все математические операции выражаются через общепринятые символы +, -, *, /, ^
- Корень квадратный √¯ ≡ sqrt, степень корня ≡ x^(2/3), (x-1)^(1/3)
число π ≡ pi, число e ≡ exp(1), ∞ ≡ infinity
ex = exp(x), log5(x) ≡ log(x,5)
Тригонометрические функции: cos(x), sin(x), tg(x), ctg(x), arccos(x), arcsin(x), arctg(x), arcctg(x)
Свойства целевой функции потребления
- Функция U(X) является возрастающей функцией всех своих аргументов, т.е. увеличение потребления любого блага при неизменном уровне потребления всех других благ увеличивает значение данной функции. Поэтому более удаленная от начала координат кривая безразличия соответствует большему значению целевой функции потребления, а сам процесс максимизации этой функции на некотором ограниченном множестве допустимых векторов У можно интерпретировать как нахождение допустимой точки, принадлежащей кривой безразличия, максимально удаленной от начала координат;
- Кривые безразличия не могут пересекаться, т.е. через одну точку пространства благ (товаров, услуг) можно провести только одну поверхность безразличия. В противном случае один и тот же набор благ одновременно соответствовал бы нескольким разным уровням материального благосостояния;
- Кривые безразличия имеют отрицательный наклон к каждой оси координат, при этом абсолютный наклон кривых уменьшается при движении в положительном направлении по каждой оси, т.е. кривые безразличия являются выпуклыми кривыми.
Свойства целевой функции потребления
Пример №1. Пусть для двух товаров целевая функция потребления имеет вид U(X) = x1x23, вектор цен равен Р = (3; 6); величина дохода равна Z. Так как в данном случае предельные полезности имеют вид:x23 = 3λ
3x1x22 = 6λ
3x1 + 6x2 = Z
После подстановки первого уравнения во второе получим Зx1x22 = 2x23. Выразив из третьего уравнения 3x1 и подставив в последнее равенство, будем иметь (Z - 6x2)x22 = 2x23, откуда можно получить, что x2 = 1/8 Z. Подставив этот результат в третье уравнение, получим x1 = 1/12 Z. Таким образом, для данного примера функции спроса на товары x1 и y2 от дохода Z имеют вид:
Пример №2. Найдите функции спроса и оптимальный потребительский набор при ценах первого и второго блага соответственно 4 и 6 ден. ед. и доходе потребителя 100 ден.ед., если функция предпочтений потребителя u(x1,x2)=2(10-x1)2+3(20-x2)2 → min.
Пример №3. Решите задачу потребительского выбора, найдя функции спроса, при ценах благ p1=5, p2=1 и доходе I=40, со следующей функцией полезности U=(x1-1)1/2*(x2-6)3/4 → max.
Решение. Для двух товаров целевая функция потребления имеет вид:
U = (x1-1)1/2•(x2-6)3/4
Вектор цен равен Р = (5; 1); величина дохода равна 40.
Предельные полезности имеют вид:
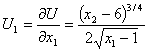
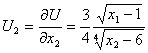
D = 40
Необходимые условия оптимума дают следующую систему уравнений (λ — множитель Лагранжа):
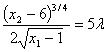

5x1 + x2 = 40
После подстановки первого уравнения во второе получим:

Выразив из третьего уравнения x1 и подставив в последнее равенство, будем иметь:
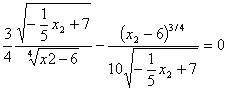
Решая его относительно x2 получим: x2 = 117/5
При x2 = 117/5: x1 = 83/25
Точка спроса: (83/25; 117/5).
Чтобы найти функции спроса x1 = f(I), x2 = f(I), аналогично составляем систему уравнений:
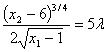

5x1 + x2 = I
Решая ее, получаем:
x1 = 1/25(2I+3)
x2 = 3/5(I-1)
Пример №4. Найдите оптимальный потребительский набор, если функция предпочтений потребителя u(x1,x2)=(x1-4)1/4(x2-10)3/4, цены первого и второго товара соответственно 25 и 10 ден. ед., доход потребителя 400 ден.ед.
Для решения, используем функцию спроса модели Стоуна: 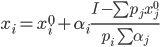
В нашем случае: x10 = 4; x20 = 10; α1 = 1/4; α2 = 3/4
Используя формулу, получаем: x1 = 4 + 1/4 • (400 - 25 • 4 - 10 • 10)/(25(1/4 + 3/4)) = 6
x2 = 10 + 3/4 • (400 - 25 • 4 - 10 • 10)/(10(1/4 + 3/4)) = 25
Откуда: Umax = (6-4)1/4(25-10)3/4 = 9.06412613