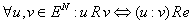Общая полезность
Общая полезность - удовлетворение, которое получают от потребления определенного набора товара или услуги.Предельная полезность - это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.
Производная по количеству Q
Например, TU = x*y. Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Например, TU = 10x2 + 2x + 2. Mux = d(10x2 + 2x + 2)/dx = 20x + 2
Функция полезности - функция, показывающая убывание полезности блага с ростом его количества:
Условия равновесия потребителя
Условия равновесия потребителя можно выразить формулой:Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.
Пример задачи на нахождение оптимального набора покупок при заданной общей полезности.
Пример задачи на нахождение оптимального набора товаров при заданной функции полезности.
Кривая безразличия
Кривая безразличия - это множество точек на кривой, которые показывают различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.Предельная норма замещения (marginal rate of substitution - MRS) - количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу:
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
Бюджетная линия
Бюджетная линия представляет собой прямую линию с отрицательным наклоном, графически отображающую множество наборов из двух товаров, требующих одинаковых затрат на их потребление. Она показывает, какие потребительские наборы можно приобрести за данную сумму денег.Px - цена блага Х;
Py - цена блага Y;
X,Y - составляют соответственно купленные количества благ.
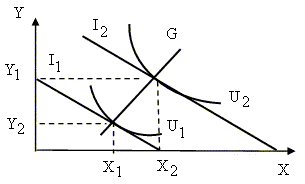
Y = -Px/PyX + I/Py
где -Px/Py - угол наклона прямой к оси абсцисс.
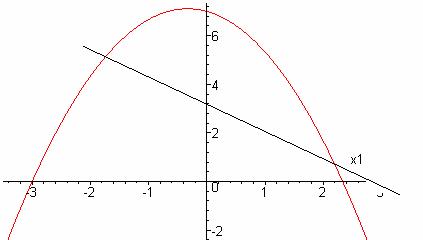
Местоположение точек потребительского равновесия на бюджетных линиях
На рисунке представлены две кривые безразличия покупателя, покупающего шоколад и сыр, а также прежняя бюджетная линия АВ и новая АС. Точки М и N - точки потребительского равновесия при денежном доходе равном 120 руб.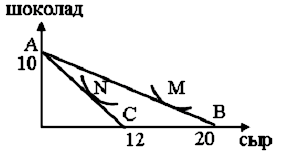
а) найти цену шоколадки и цену сыра;
б) объяснить, чем обусловлен сдвиг бюджетной линии АВ в положение АС;
в) найти угол наклона бюджетной линии АВ и АС;
г) объяснить, чем обусловлено местоположение точек потребительского равновесия на бюджетных линиях.|а) цена шоколадки:
б) Pсыр = I / Qсыр(AC) = 120/12 = 10
Сдвиг обусловлен повышением цены на сыр.
в) Угол наклона АС
Уравнение бюджтеной линии
Y = I - Px / Py X
k = Px / Py - угол наклона
Угол наклона АB
г) Местоположение точек потребительского равновесия на бюджетных линиях обусловлено равновесие потребителя (оптимальное сочетание двух товаров - шоколада и сыра) при фиксированном бюджете средств.
Пример решения определения оптимума потребителя
Пример №1. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны Px=2 руб. и Py=4 руб. Найдите равновесный набор.Решение: Из условия равновесия потребителя: Mux / Muy = Px / Py получаем: Mux = d(x*y)/dx = y; Muy = d(x*y)/dy = x
Тогда: y / x = 2 / 4 = 1/2 или y = 1/2x
Для наших данных уравнение бюджетной линии запишем как:
80 = 2x + 4y = 2x + 4*1/2x = 4x
Откуда: x = 20 ед., y = 1/2*20 = 10 ед.
Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.
Пример №2. Потребитель тратит 600 рублей в месяц на приобретение двух товаров. Цена товара Х - 20 рублей, а товара Y - 10 рублей. Задана функция полезности потребителя U = ХY. Составить уравнение бюджетной линии. Найти предельную норму замещения. Определить оптимум потребителя. Представить графически. Если цена товара Х уменьшится на 5 руб., на сколько единиц изменится объем спроса данного товара всего?|Уравнение бюджетной линии:
Предельная полезность товаров:
Оптимум потребителя достигается при равенстве:
Предельная норма замещения
Выразим y через x.
Подставим в уравнение бюджетной линии:
Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.
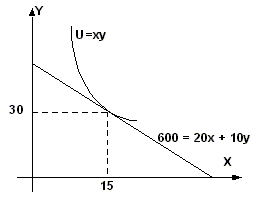
Проверка: 20 х 15 + 10 х 30 = 300 + 300 = 600.
При уменьшении цены товара X на 5 руб.
Px = 20 - 5 = 15
Найдем новый оптимум потребителя.
Спрос на товар Х увеличился на 2.14 (17.14 - 15)
Проверка: 15 х 17.14 + 10 х 34.29 = 257.1 + 342.9 = 600.
Пример выбора рациональных покупок
Сделайте наиболее рациональные покупки, если есть три товара А,В,С, руководствуясь возможностью потратить 23 000 рублей.| Количество единиц | 1 | 2 | 3 | 4 | 5 |
| Общая полезность (А) | 5000 | 6200 | 7300 | 8200 | 9000 |
| Общая полезность (В) | 3000 | 5500 | 7900 | 10000 | 12000 |
| Общая полезность (С) | 2500 | 4000 | 5300 | 6400 | 7000 |
Цены: Р(А) = 1500 руб.; Р(В) = 4000 руб.; Р(С) = 1000 руб.
Уравнение бюджетной линии
Потребитель выбирает максимум полезности из условия:
Предельная полезность MU определяется по формуле:
| Количество единиц | 1 | 2 | 3 | 4 | 5 |
| Общая полезность (А) | 5000 | 6200 | 7300 | 8200 | 9000 |
| Общая полезность (В) | 3000 | 5500 | 7900 | 10000 | 12000 |
| Общая полезность (С) | 2500 | 4000 | 5300 | 6400 | 7000 |
| MU(A) | - | 1200 | 1100 | 900 | 800 |
| MU(B) | - | 2500 | 2400 | 2100 | 2000 |
| MU(C) | - | 1500 | 1300 | 1100 | 600 |
| MU(A)/ P(A) | - | 0,80 | 0,73 | 0,60 | 0,53 |
| MU(B) /P(B) | - | 0,63 | 0,60 | 0,53 | 0,50 |
| MU(C) /P(C) | - | 1,50 | 1,30 | 1,10 | 0,60 |
Из таблицы выбираем оптимальный объем для товаров (MU = 0,6)
A = 4; B = 3; C = 5.
Проверка:
Утилитарное решение и решение, оптимальное по Нэшу
Определить утилитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны u1 = х1 + 3, u2= 3х2 - 2 при х1 + x2 = 3 . Проверить независимость от масштаба для указанных ПКБ, если функция полезности первого агента была уменьшена в три раза.Решение. Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1 + 3 = 3x2 - 2. Учитывая, что x2 = 3- x1, получаем x2 = 2, тогда x1 = 1. Вектор полезностей (4,4).
Утилитарное решение находим, максимизируя сумму полезностей агентов: x1 + 3 + 3x2 - 2 → max, подставив x1 вместо x2, получаем 4x2 + 1 → max. Рассматриваемая функция возрастает от x1 и достигает своего максимума при x1 = 3, тогда x2 = 0. Здесь вектор полезностей (1,1).
Независимость от масштаба
Определим эгалитарное решение, для этого должно выполняться условие u1 = u2 или x1/3 + 1 = 3x2 - 2. Учитывая, что x2 = 3- x1, получаем 10/3 x1 - 6 = 0, тогда x1 = 9/5, то x2 = 6/5. Вектор полезностей (8/5,8/5).
Множество допустимых распределений пары продуктов на неотрицательные количества определяется так:x1,x2 0, x1 + x1 = a, x2 = b.
Максимизируя ФКП Нэша, мы выбираем эффективное распределение. Оптимальное распределение определяется как решение задачи:
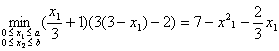
Видим, что соблюдается условия:
а) 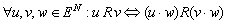 ,
,
б)